Manipulating Spectra

While there are myriad ways you might want to alter a spectrum, specutils provides some specific functionality that is commonly used in astronomy. These tools are detailed here, but it is important to bear in mind that this is not intended to be exhaustive - the point of specutils is to provide a framework you can use to do your data analysis. Hence the functionality described here is best thought of as pieces you might string together with your own functionality to build a tailor-made spectral analysis environment.

In general, however, specutils is designed around the idea that spectral manipulations generally yield new spectrum objects, rather than in-place operations. This is not a true restriction, but is a guideline that is recommended primarily to keep you from accidentally modifying a spectrum you didn’t mean to change.

Smoothing

Specutils provides smoothing for spectra in two forms: 1) convolution based using smoothing astropy.convolution and 2) median filtering using the scipy.signal.medfilt(). Each of these act on the flux of the Spectrum1D object.

Note

Specutils smoothing kernel widths and standard deviations are in units of pixels and not Quantity.

Convolution Based Smoothing

While any kernel supported by astropy.convolution will work (using the convolution_smooth function), several commonly-used kernels have convenience functions wrapping them to simplify the smoothing process into a simple one-line operation. Currently implemented are: box_smooth() (Box1DKernel), gaussian_smooth() (Gaussian1DKernel), and trapezoid_smooth() (Trapezoid1DKernel). Note that, although these kernels are 1D, they can be applied to higher-dimensional data (e.g. spectral cubes), in which case the data will be smoothed only along the spectral dimension.

>>> from specutils import Spectrum1D
>>> import astropy.units as u
>>> import numpy as np
>>> from specutils.manipulation import box_smooth, gaussian_smooth, trapezoid_smooth

>>> spec1 = Spectrum1D(spectral_axis=np.arange(1, 50) * u.nm,
...                    flux=np.random.default_rng(12345).random(49)*u.Jy)
>>> spec1_bsmooth = box_smooth(spec1, width=3)
>>> spec1_gsmooth = gaussian_smooth(spec1, stddev=3)
>>> spec1_tsmooth = trapezoid_smooth(spec1, width=3)
>>> gaussian_smooth(spec1, stddev=3) 
<Spectrum1D(flux=[0.25860917267578276 ... 0.15868783272966752] Jy (shape=(49,), mean=0.48009 Jy); spectral_axis=<SpectralAxis [ 1.  2.  3. ... 47. 48. 49.] nm> (length=49))>

Each of the specific smoothing methods create the appropriate astropy.convolution.convolve kernel and then call a helper function convolution_smooth() that takes the spectrum and an astropy 1D kernel. So, one could also do:

>>> from astropy.convolution import Box1DKernel
>>> from specutils.manipulation import convolution_smooth

>>> box1d_kernel = Box1DKernel(width=3)

>>> spec1 = Spectrum1D(spectral_axis=np.arange(1, 50) * u.nm,
...                    flux=np.random.default_rng(12345).random(49) * u.Jy)
>>> convolution_smooth(spec1, box1d_kernel) 
<Spectrum1D(flux=[0.1813647873923075 ... 0.1201562712204726] Jy (shape=(49,), mean=0.49378 Jy); spectral_axis=<SpectralAxis [ 1.  2.  3. ... 47. 48. 49.] nm> (length=49))>

In this case, the spec1_bsmooth2 result should be equivalent to the spec1_bsmooth in the section above (assuming the flux data of the input spec is the same). Note that, as in the case of the kernel-specific functions, a 1D kernel can be applied to a multi-dimensional spectrum and will smooth that spectrum along the spectral dimension. In the case of convolution_smooth(), one can also input a higher-dimensional kernel that matches the dimensionality of the data.

The uncertainties are propagated using a standard “propagation of errors” method, if the uncertainty is defined for the spectrum and it is one of StdDevUncertainty, VarianceUncertainty or InverseVariance. But note that this does not consider covariance between points.

Median Smoothing

The median based smoothing is implemented using scipy.signal.medfilt and has a similar call structure to the convolution-based smoothing methods. This method applys the median filter across the flux.

Note

This method is not flux conserving and errors are not propagated.

>>> from specutils.manipulation import median_smooth

>>> spec1 = Spectrum1D(spectral_axis=np.arange(1, 50) * u.nm,
...                    flux=np.random.default_rng(12345).random(49) * u.Jy)
>>> median_smooth(spec1, width=3) 
<Spectrum1D(flux=[0.22733602246716966 ... 0.005022333717131788] Jy (shape=(49,), mean=0.48620 Jy); spectral_axis=<SpectralAxis [ 1.  2.  3. ... 47. 48. 49.] nm> (length=49))>

Resampling

specutils contains several classes for resampling the flux in a Spectrum1D object. Currently supported methods of resampling are integrated flux conserving with FluxConservingResampler, linear interpolation with LinearInterpolatedResampler, and cubic spline with SplineInterpolatedResampler. Each of these classes takes in a Spectrum1D and a user defined output dispersion grid, and returns a new Spectrum1D with the resampled flux. Currently the resampling classes expect the new dispersion grid unit to be the same as the input spectrum’s dispersion grid unit. Additionally, all resamplers take an optional extrapolation_treatment keyword which can be nan_fill, zero_fill, or truncate, to determine what to do with output wavelength bins that have no overlap with the original spectrum.

If the input Spectrum1D contains an uncertainty, FluxConservingResampler will propogate the uncertainty to the final output Spectrum1D. However, the other two implemented resampling classes (LinearInterpolatedResampler and SplineInterpolatedResampler) will ignore any input uncertainty.

Here’s a set of simple examples showing each of the three types of resampling:

First are the imports we will need as well as loading in the example data:

>>> from astropy.io import fits
>>> from astropy import units as u
>>> import numpy as np
>>> from matplotlib import pyplot as plt
>>> from astropy.visualization import quantity_support
>>> quantity_support()  # for getting units on the axes below  

>>> filename = 'https://data.sdss.org/sas/dr16/sdss/spectro/redux/26/spectra/1323/spec-1323-52797-0012.fits'
>>> # The spectrum is in the second HDU of this file.
>>> with fits.open(filename) as f:  
...     specdata = f[1].data[1020:1250]  

Then we re-format this dataset into astropy quantities, and create a Spectrum1D object:

>>> from specutils import Spectrum1D
>>> lamb = 10**specdata['loglam'] * u.AA 
>>> flux = specdata['flux'] * 10**-17 * u.Unit('erg cm-2 s-1 AA-1') 
>>> input_spec = Spectrum1D(spectral_axis=lamb, flux=flux) 

>>> f, ax = plt.subplots()  
>>> ax.step(input_spec.spectral_axis, input_spec.flux) 

(Source code, png, hires.png, pdf)

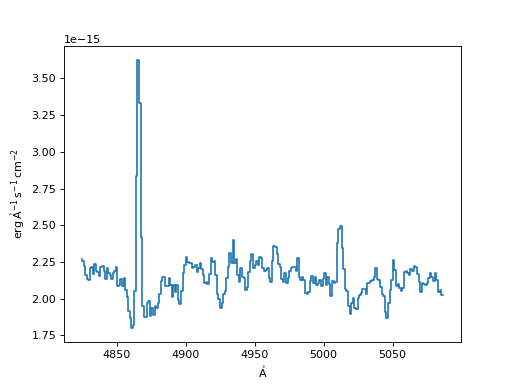
Now we show examples and plots of the different resampling currently available.

>>> from specutils.manipulation import FluxConservingResampler, LinearInterpolatedResampler, SplineInterpolatedResampler
>>> new_disp_grid = np.arange(4800, 5200, 3) * u.AA

Flux Conserving Resampler:

>>> fluxcon = FluxConservingResampler()
>>> new_spec_fluxcon = fluxcon(input_spec, new_disp_grid) 
>>> f, ax = plt.subplots()  
>>> ax.step(new_spec_fluxcon.spectral_axis, new_spec_fluxcon.flux) 

(Source code, png, hires.png, pdf)

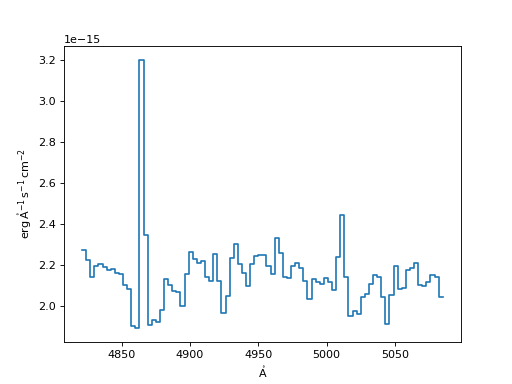
Linear Interpolation Resampler:

>>> linear = LinearInterpolatedResampler()
>>> new_spec_lin = linear(input_spec, new_disp_grid)  
>>> f, ax = plt.subplots()  
>>> ax.step(new_spec_lin.spectral_axis, new_spec_lin.flux) 

(Source code, png, hires.png, pdf)

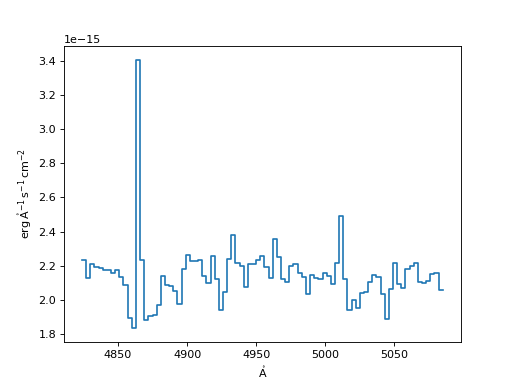
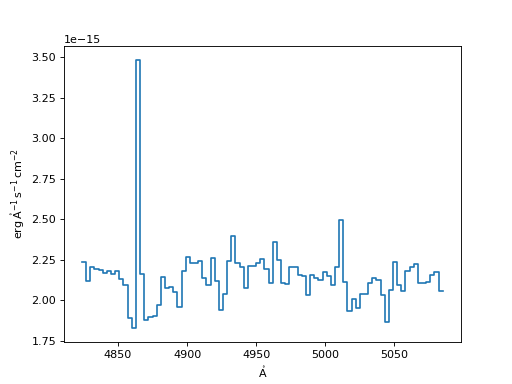
Spline Resampler:

>>> spline = SplineInterpolatedResampler()
>>> new_spec_sp = spline(input_spec, new_disp_grid)  
>>> f, ax = plt.subplots()  
>>> ax.step(new_spec_sp.spectral_axis, new_spec_sp.flux) 

(Source code, png, hires.png, pdf)

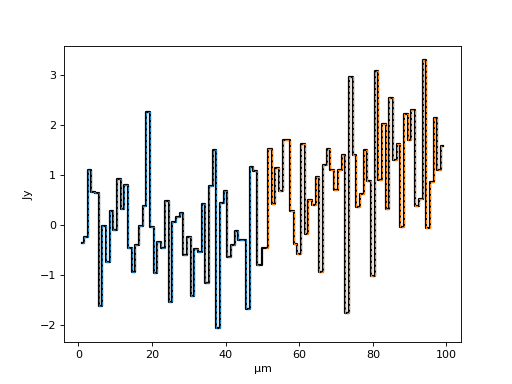
Splicing/Combining Multiple Spectra

The resampling functionality detailed above is also the default way specutils supports splicing multiple spectra together into a single spectrum. This can be achieved as follows:

>>> spec1 = Spectrum1D(spectral_axis=np.arange(1, 50) * u.micron, flux=np.random.randn(49)*u.Jy)
>>> spec2 = Spectrum1D(spectral_axis=np.arange(51, 100) * u.micron, flux=(np.random.randn(49)+1)*u.Jy)

>>> new_spectral_axis = np.concatenate([spec1.spectral_axis.value, spec2.spectral_axis.to_value(spec1.spectral_axis.unit)]) * spec1.spectral_axis.unit

>>> resampler = LinearInterpolatedResampler(extrapolation_treatment='zero_fill')
>>> new_spec1 = resampler(spec1, new_spectral_axis)
>>> new_spec2 = resampler(spec2, new_spectral_axis)

>>> final_spec = new_spec1 + new_spec2

Yielding a spliced spectrum (the solid line below) composed of the splice of two other spectra (dashed lines):

>>> f, ax = plt.subplots()  
>>> ax.step(final_spec.spectral_axis, final_spec.flux, where='mid', c='k', lw=2) 
>>> ax.step(spec1.spectral_axis, spec1.flux, ls='--', where='mid', lw=1) 
>>> ax.step(spec2.spectral_axis, spec2.flux, ls='--', where='mid', lw=1) 

(Source code, png, hires.png, pdf)

Uncertainty Estimation

Some of the machinery in specutils (e.g. snr) requires an uncertainty to be present. While some data reduction pipelines generate this as part of the reduction process, sometimes it’s necessary to estimate the uncertainty in a spectrum using the spectral data itself. Currently specutils provides the straightforward noise_region_uncertainty function.

First we build a spectrum like that used in Analysis, but without a known uncertainty:

>>> from astropy.modeling import models
>>> spectral_axis = np.linspace(10, 1, 200) * u.GHz
>>> spectral_model = models.Gaussian1D(amplitude=3*u.Jy, mean=5*u.GHz, stddev=0.8*u.GHz)
>>> flux = spectral_model(spectral_axis)
>>> flux += np.random.default_rng(42).normal(0., 0.2, spectral_axis.shape) * u.Jy
>>> noisy_gaussian = Spectrum1D(spectral_axis=spectral_axis, flux=flux)

Now we estimate the uncertainty from the region that does not contain the line:

>>> from specutils import SpectralRegion
>>> from specutils.manipulation import noise_region_uncertainty
>>> noise_region = SpectralRegion([(10, 7), (3, 0)] * u.GHz)
>>> spec_w_unc = noise_region_uncertainty(noisy_gaussian, noise_region)
>>> spec_w_unc.uncertainty[::20] 
StdDevUncertainty([0.17501999, 0.17501999, 0.17501999, 0.17501999,
                   0.17501999, 0.17501999, 0.17501999, 0.17501999,
                   0.17501999, 0.17501999])

Or similarly, expressed in pixels:

>>> noise_region = SpectralRegion([(0, 25), (175, 200)]*u.pix)
>>> spec_w_unc = noise_region_uncertainty(noisy_gaussian, noise_region)
>>> spec_w_unc.uncertainty[::20]  
StdDevUncertainty([0.17547552, 0.17547552, 0.17547552, 0.17547552,
                   0.17547552, 0.17547552, 0.17547552, 0.17547552,
                   0.17547552, 0.17547552])

S/N Threshold Mask

It is useful to be able to find all the spaxels in an ND spectrum in which the signal to noise ratio is greater than some threshold. This method implements this functionality so that a Spectrum1D object, SpectrumCollection or an NDData derived object may be passed in as the first parameter. The second parameter is a floating point threshold.

For example, first a spectrum with flux and uncertainty is created, and then call the snr_threshold method:

>>> import numpy as np
>>> from astropy.nddata import StdDevUncertainty
>>> import astropy.units as u
>>> from specutils import Spectrum1D
>>> from specutils.manipulation import snr_threshold
>>> wavelengths = np.arange(0, 10)*u.um
>>> rng = np.random.default_rng(42)
>>> flux = 100*np.abs(rng.standard_normal(10))*u.Jy
>>> uncertainty = StdDevUncertainty(np.abs(rng.standard_normal(10))*u.Jy)
>>> spectrum = Spectrum1D(spectral_axis=wavelengths, flux=flux, uncertainty=uncertainty)
>>> spectrum_masked = snr_threshold(spectrum, 50)
>>> # To create a masked flux array
>>> flux_masked = spectrum_masked.flux
>>> flux_masked[spectrum_masked.mask] = np.nan

The output spectrum_masked is a shallow copy of the input spectrum with the mask attribute set to False where the S/N is greater than 50 and True elsewhere. It is this way to be consistent with astropy.nddata.

Note

The mask attribute is the only attribute modified by snr_threshold(). To retrieve the masked flux data use spectrum.masked.flux_masked.

Shifting

In addition to resampling, you may sometimes wish to simply shift the spectral_axis of a spectrum (a la the specshift iraf task). There is no explicit function for this because it is a basic transform of the spectral_axis. Therefore one can use a construct like this:

>>> from specutils import Spectrum1D
>>> wavelengths = np.arange(0, 10) * u.um
>>> flux = 100 * np.abs(np.random.default_rng(42).standard_normal(10)) * u.Jy
>>> spectrum = Spectrum1D(spectral_axis=wavelengths, flux=flux)
>>> spectrum  
<Spectrum1D(flux=<Quantity [ 30.47170798, 103.99841062,  75.04511958,  94.05647164,
           195.10351887, 130.21795069,  12.78404032,  31.62425923,
             1.68011575,  85.30439276] Jy> (shape=(10,), mean=76.02860 Jy); spectral_axis=<SpectralAxis [0. 1. 2. ... 7. 8. 9.] um> (length=10))>

>>> shift = 12300 * u.AA
>>> new_spec = Spectrum1D(spectral_axis=spectrum.spectral_axis + shift, flux=spectrum.flux)
>>> new_spec  
<Spectrum1D(flux=<Quantity [ 30.47170798, 103.99841062,  75.04511958,  94.05647164,
           195.10351887, 130.21795069,  12.78404032,  31.62425923,
             1.68011575,  85.30439276] Jy> (shape=(10,), mean=76.02860 Jy); spectral_axis=<SpectralAxis [ 1.23  2.23  3.23 ...  8.23  9.23 10.23] um> (length=10))>

Replacing a region

A specific wavelength region of a spectrum can be replaced with a model fitted to that region by using the model_replace function. By default, the function uses a cubic spline to model the specified region. Alternatively, it can use a previously fitted model from modeling.

The simplest way to use model_replace is to provide a list or array with the spline knots:

>>> from specutils.manipulation.model_replace import model_replace
>>> wave_val = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
>>> flux_val = np.array([2, 4, 6, 8, 10, 12, 14, 16, 18, 20])
>>> input_spectrum = Spectrum1D(spectral_axis=wave_val * u.AA, flux=flux_val * u.mJy)
>>> spline_knots = [3.5, 4.7, 6.8, 7.1] * u.AA
>>> result = model_replace(input_spectrum, None, model=spline_knots)
>>> result
<Spectrum1D(flux=<Quantity [ 2.,  4.,  6.,  8., 10., 12., 14., 16., 18., 20.] mJy> (shape=(10,), mean=11.00000 mJy); spectral_axis=<SpectralAxis [ 1.  2.  3. ...  8.  9. 10.] Angstrom> (length=10))>

The default behavior is to keep the data outside the replaced region unchanged. Alternatively, the spectrum outside the replaced region can be filled with zeros:

>>> spline_knots = [3.5, 4.7, 6.8, 7.1] * u.AA
>>> result = model_replace(input_spectrum, None, model=spline_knots, extrapolation_treatment='zero_fill')
>>> result
<Spectrum1D(flux=<Quantity [ 0.,  0.,  0.,  8., 10., 12., 14.,  0.,  0.,  0.] mJy> (shape=(10,), mean=4.40000 mJy); spectral_axis=<SpectralAxis [ 1.  2.  3. ...  8.  9. 10.] Angstrom> (length=10))>

One can define the spline knots by providing an instance of SpectralRegion, and the number of knots to be evenly spread along the region:

>>> from specutils import SpectralRegion
>>> region = SpectralRegion(3.5*u.AA, 7.1*u.AA)
>>> result = model_replace(input_spectrum, region, model=4)
>>> result
<Spectrum1D(flux=<Quantity [ 2.,  4.,  6.,  8., 10., 12., 14., 16., 18., 20.] mJy> (shape=(10,), mean=11.00000 mJy); spectral_axis=<SpectralAxis [ 1.  2.  3. ...  8.  9. 10.] Angstrom> (length=10))>

A model fitted over the region can also be used to replace the spectrum flux values:

>>> from astropy.modeling import models
>>> from specutils.fitting import fit_lines
>>> flux_val = np.array([1, 1.1, 0.9, 4., 10., 5., 2., 1., 1.2, 1.1])
>>> input_spectrum = Spectrum1D(spectral_axis=wave_val * u.AA, flux=flux_val * u.mJy)
>>> model = models.Gaussian1D(10, 5.6, 1.2)
>>> fitted_model = fit_lines(input_spectrum, model)
>>> region = SpectralRegion(3.5*u.AA, 7.1*u.AA)
>>> result = model_replace(input_spectrum, region, model=fitted_model)
>>> result  
<Spectrum1D(flux=<Quantity [1.        , 1.1       , 0.9       , 4.40801804, 9.58271877,
           5.61238054, 0.88556096, 1.        , 1.2       , 1.1       ] mJy> (shape=(10,), mean=2.67887 mJy); spectral_axis=<SpectralAxis [ 1.  2.  3. ...  8.  9. 10.] Angstrom> (length=10))>

Reference/API

Functions

box_smooth(spectrum, width)	Smooth a Spectrum1D instance along the spectral axis based on a astropy.convolution.Box1DKernel kernel.
convolution_smooth(spectrum, kernel)	Apply a convolution based smoothing to the spectrum.
excise_regions(spectrum, regions[, exciser])	Method to remove or replace the flux in the defined regions of the spectrum depending on the function provided in the exciser argument.
extract_bounding_spectral_region(spectrum, ...)	Extract the entire bounding region that encompasses all sub-regions contained in a multi-sub-region instance of SpectralRegion.
extract_region(spectrum, region[, ...])	Extract a region from the input Spectrum1D defined by the lower and upper bounds defined by the region instance.
gaussian_smooth(spectrum, stddev)	Smooth a Spectrum1D instance along the spectral axis based on a astropy.convolution.Gaussian1DKernel.
linear_exciser(spectrum, region)	Basic spectral excise method where the spectral region defined by the parameter region (a SpectralRegion) will result in the flux between those regions set to a linear ramp of the two points immediately before and after the start and end of the region.
median_smooth(spectrum, width)	Smoothing based on a median filter.
noise_region_uncertainty(spectrum, ...[, ...])	Generates a new spectrum with an uncertainty from the noise in a particular region of the spectrum.
snr_threshold(spectrum, value[, op])	Calculate the mean S/N of the spectrum based on the flux and uncertainty in the spectrum.
spectral_slab(spectrum, lower, upper)	Extract a slab from the input Spectrum1D defined by the lower and upper bounds defined by the region instance.
spectrum_from_model(model_input, spectrum)	This method will create a Spectrum1D object with the flux defined by calling the input model.
trapezoid_smooth(spectrum, width)	Smooth a Spectrum1D instance along the spectral axis based on a astropy.convolution.Trapezoid1DKernel kernel.

Classes

FluxConservingResampler([...])	This resampling algorithm conserves overall integrated flux (as opposed to flux density).
LinearInterpolatedResampler([...])	Resample a spectrum onto a new spectral_axis using linear interpolation.
ResamplerBase([extrapolation_treatment])	Base class for resample classes.
SplineInterpolatedResampler([...])	This resample algorithim uses a cubic spline interpolator.

Class Inheritance Diagram